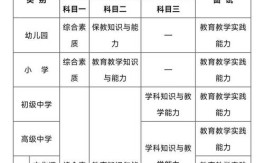
考试结构与分值分布（以笔试《学科知识与教学能力》为例）

2025年初中数学教师资格证笔试科目三《学科知识与教学能力》主要包括三大部分：

1. 学科知识：约占30%-40%
2. 课程知识：约占20%-30%
3. 教学知识：约占30%-40%

总分150分,考试时间120分钟。

各部分核心考点与典型题型分析

第一部分：学科知识

这部分主要考察你对高等数学、大学数学和初中数学基础知识的掌握程度，以及将这些知识融会贯通的能力。

高等数学基础

• 核心考点：
  • 数学分析：极限、连续、导数与微分、积分（定积分、不定积分），这是考察的重中之重。
  • 线性代数：矩阵、行列式、线性方程组。
  • 概率论与数理统计：随机变量、概率分布（特别是正态分布）、数字特征（期望、方差）。
• 典型题型：
  • 计算题：求函数的极限、求导数、求定积分，这是最常见的题型。
  • 概念辨析题：考察“连续”、“可导”、“可积”之间的关系。
  • 应用题：利用导数求函数的极值、最值；利用定积分求平面图形的面积。
  • 证明题：证明一个数列的极限，或证明某个不等式。

【典型例题1（计算题）】 求函数 $f(x) = \frac{x^2 - 1}{x - 1}$ 在 $x \to 1$ 时的极限。

• 解析：这是典型的极限计算题，直接代入 $x=1$ 会导致分母为0，属于“0/0”型未定式，需要先化简： $f(x) = \frac{(x-1)(x+1)}{x-1} = x+1$ （当 $x \neq 1$ 时） $\lim{x \to 1} f(x) = \lim{x \to 1} (x+1) = 2$。 考察点：极限的计算方法（因式分解约分）。

【典型例题2（应用题）】 一个底面半径为 $r$，高为 $h$ 的圆锥形漏斗，求其体积。

• 解析：这考察的是定积分的应用（旋转体的体积）。
  1. 建立坐标系：以圆锥的顶点为原点，高所在直线为x轴。
  2. 找到母线方程：在 $x=h$ 处，半径为 $r$，所以母线为 $y = \frac{r}{h}x$。
  3. 体积公式：$V = \pi \int_0^h [f(x)]^2 dx = \pi \int_0^h (\frac{r}{h}x)^2 dx = \pi \frac{r^2}{h^2} \int_0^h x^2 dx = \pi \frac{r^2}{h^2} [\frac{x^3}{3}]_0^h = \pi \frac{r^2}{h^2} \cdot \frac{h^3}{3} = \frac{1}{3}\pi r^2 h$。 考察点：定积分的几何应用，建立数学模型的能力。

初中数学核心知识

• 核心考点：
  • 数与代数：实数、代数式、方程（一元一次、一元二次、分式、方程组）、不等式、函数（一次、二次、反比例、指数、对数）。
  • 图形与几何：三角形、四边形、圆、立体图形、尺规作图、图形的变换（平移、旋转、对称、相似）。
  • 统计与概率：数据的收集与整理、统计图表、平均数、中位数、众数、方差、概率的初步认识。
• 典型题型：
  • 解题能力题：给出一个复杂的初中数学问题，要求你给出完整的解题过程，并指出其中蕴含的数学思想方法（如数形结合、分类讨论、转化与化归）。
  • 知识拓展题：将初中二次函数的顶点式与大学导数求极值的方法联系起来。

【典型例题3（解题能力题）】 已知关于 $x$ 的方程 $kx^2 - 2(k+1)x + k - 2 = 0$ 有两个不相等的实数根，求 $k$ 的取值范围。

• 解析：
  1. 判断方程类型：当 $k=0$ 时，方程为 $-2x - 2 = 0$，只有一个实数根，不符合题意。$k \neq 0$。
  2. 使用判别式：对于一元二次方程 $ax^2+bx+c=0$，有两个不等实根的条件是 $\Delta = b^2 - 4ac > 0$。
  3. 计算：这里 $a=k$, $b=-2(k+1)$, $c=k-2$。 $\Delta = [-2(k+1)]^2 - 4 \cdot k \cdot (k-2) = 4(k^2 + 2k + 1) - 4k^2 + 8k = 4k^2 + 8k + 4 - 4k^2 + 8k = 16k + 4$。
  4. 解不等式：$\Delta > 0 \Rightarrow 16k + 4 > 0 \Rightarrow 16k > -4 \Rightarrow k > -\frac{1}{4}$。
  5. 综合条件：结合第一步 $k \neq 0$ 和第四步 $k > -\frac{1}{4}$，最终得出 $k$ 的取值范围是 $k > -\frac{1}{4}$ 且 $k \neq 0$。 考察点：分类讨论思想、一元二次方程根的判别式的应用。

第二部分：课程知识

这部分考察你对《义务教育数学课程标准（2011年版）》的理解和运用能力。

• 核心考点：
  • 课程性质与基本理念：“人人都能获得良好的数学教育，不同的人在数学上得到不同的发展”等核心理念。
  • 课程目标：从“知识与技能”、“过程与方法”、“情感态度与价值观”三个维度来阐述。
  • ：数与代数、图形与几何、统计与概率、综合与实践四大领域的具体内容和要求。
  • 课程实施建议：教学建议、评价建议、教材使用建议。
• 典型题型：
  • 简答题/论述题：阐述你对某个课程理念的理解。
  • 案例分析题：给出一个教学片段，要求你用课程标准的理念去分析其优点或不足。
  • 设计题：根据某个课程内容，设计一个符合课程标准的探究式学习活动。

【典型例题4（简答题）】 简述《义务教育数学课程标准》中提出的“基本理念”之一——“学生是学习的主体，教师是学习的组织者、引导者与合作者”的内涵。

• 解析：
  • 学生是学习的主体：强调数学学习是一个主动建构的过程，而不是被动接受的过程，学生不是知识的容器，而是通过自己的观察、思考、猜想、验证、交流等方式，主动地理解和掌握数学知识、技能和思想方法。
  • 教师是学习的组织者：教师需要创设有效的问题情境，设计合理的教学活动，组织学生进行探究、讨论和合作，为学生搭建学习的“脚手架”。
  • 教师是学习的引导者：当学生在学习中遇到困难或偏离方向时，教师需要通过提问、提示、示范等方式，引导学生思考，帮助他们找到解决问题的路径，而不是直接给出答案。
  • 教师是学习的合作者：教师应放下权威的架子，以平等的身份参与到学生的学习活动中，与学生共同探索、共同进步，营造民主、和谐的课堂氛围。 考察点：对新课标理念的准确理解和语言表达能力。

第三部分：教学知识

这是考试的核心,重点考察你的教学设计、实施和评价能力。

• 核心考点：
  • 教学设计：如何确定教学目标（三维目标）、如何进行学情分析、如何选择教学方法、如何设计教学过程（导入、新授、巩固、小结、作业）、如何制作和使用教具/课件。
  • 教学实施：课堂提问技巧、课堂组织与管理、信息技术与数学教学的整合、板书设计。
  • 教学评价：形成性评价与终结性评价、评价方式的多元化（观察、谈话、作业、测验等）、如何进行试卷分析和教学反思。
• 典型题型：
  • 教学设计题（大题）：这是考试的压轴题，分值最高，通常会给出一个具体的初中数学课题（如“勾股定理的逆定理”、“一次函数的图像与性质”等），要求你完成一份完整的教学设计。
  • 案例分析题：给出一个教学案例，分析其中体现的教学原则或方法，并指出可以改进的地方。

【典型例题5（教学设计题） 请以“一元二次方程的根与系数的关系”为课题，完成以下教学设计任务：

1. 确定本节课的教学目标。
2. 设计一个引导学生发现“根与系数关系”的教学环节，并写出设计意图。
3. 说明本节课的教学重难点。

• 参考答案框架：
  1. 教学目标：
     • 知识与技能：理解并掌握一元二次方程的根与系数的关系（韦达定理），并能运用它解决相关问题。
     • 过程与方法：通过观察、猜想、归纳、证明等数学活动，体验“从特殊到一般”的数学思想方法，培养探究能力和逻辑推理能力。
     • 情感态度与价值观：在探究过程中感受数学的对称美和简洁美，激发学习数学的兴趣，培养严谨的科学态度。
  2. 教学环节设计：
     • 活动：让学生解几个特殊的一元二次方程。
       • $x^2 - 5x + 6 = 0$ (解为 $x_1=2, x_2=3$)
       • $x^2 + x - 6 = 0$ (解为 $x_1=2, x_2=-3$)
       • $x^2 - 7x = 0$ (解为 $x_1=0, x_2=7$)
     • 引导提问：
       • “请观察每个方程的二次项系数、一次项系数、常数项，再看看它的两个根 $x_1$ 和 $x_2$，你发现 $x_1+x_2$ 与方程系数有什么关系？$x_1 \cdot x_2$ 呢？”
       • “你的发现是否对所有的一元二次方程都成立？我们如何验证？”
     • 归纳与证明：引导学生猜想出 $x_1+x_2 = -\frac{b}{a}$, $x_1 \cdot x_2 = \frac{c}{a}$，并利用求根公式进行一般性证明。
     • 设计意图：通过解特殊方程，降低探究难度，让学生容易发现规律，激发其好奇心和求知欲，这个过程体现了“从特殊到一般”的归纳思想，是培养学生合情推理能力的重要环节。
  3. 教学重难点：
     • 教学重点：一元二次方程根与系数关系的理解和应用。
     • 教学难点：根与系数关系的探究过程，以及如何引导学生从特殊现象归纳出一般规律。

备考策略与建议

1. 回归教材，夯实基础：系统复习高等数学的核心概念和计算方法，这是“学科知识”部分的基石，重新梳理初中数学的所有知识点，做到“知其然，更知其所以然”。
2. 研读课标，把握方向：把《义务教育数学课程标准》作为“圣经”来读，特别是课程理念和课程目标部分，所有教学设计题都必须紧扣课标精神。
3. 精研真题，模拟演练：找近几年的真题进行练习，熟悉题型、分值分布和答题时间分配，重点练习教学设计题，形成自己的模板和思路。
4. 关注教学，勤于动笔：不要只看不练，教学设计题一定要亲手写，从教学目标、教学重难点到教学过程，完整地构思和书写，可以参考优秀教案，但最终要内化为自己的东西。
5. 积累素材，形成体系：准备一些常用的教学方法和课堂活动案例，如情境导入法、小组合作探究、数学史故事等，以便在答题时能灵活运用。

祝你备考顺利,成功上岸！