初中数学学科专业知识体系
初中数学的核心目标是培养学生的“四基”(基础知识、基本技能、基本思想、基本活动经验)和“四能”(发现问题、提出问题、分析问题、解决问题的能力),其知识体系主要围绕“数与代数”、“图形与几何”、“统计与概率”、“综合与实践”四大领域展开。

第一部分:数与代数
这是初中数学的核心,贯穿整个初中阶段,是学习其他领域的基础。
数与式
-
有理数
- 核心概念:正数、负数、数轴、相反数、绝对值、倒数。
- 运算:有理数的加、减、乘、除、乘方及其混合运算,重点掌握运算顺序和符号法则。
- 思想方法:数形结合思想(数轴是核心工具),分类讨论思想。
-
实数
- 核心概念:平方根、算术平方根、立方根、无理数、实数。
- 运算:实数的四则运算,零指数幂、负整数指数幂,科学记数法。
- 联系:有理数与实数的关系,实数与数轴上的点一一对应。
-
整式与分式
 (图片来源网络,侵删)
(图片来源网络,侵删)- 整式
- 概念:单项式、多项式、同类项、合并同类项、去括号与添括号。
- 运算:整式的加、减、乘(乘法公式:平方差、完全平方)、除法、因式分解(提公因式法、公式法、十字相乘法)。
- 分式
- 概念:分式、最简分式、最简公分母。
- 性质与运算:分式的基本性质、分式的加、减、乘、除运算。
- 思想方法:转化思想(分式运算整式化),整体思想。
- 整式
-
二次根式
- 概念:二次根式、最简二次根式、同类二次根式。
- 性质与运算:$\sqrt{a^2}=|a|$,二次根式的加、减、乘、除运算。
- 联系:与实数、整式运算的联系与区别。
方程与不等式
-
方程
- 一元一次方程:解法、应用(行程、工程、配套、分配等问题)。
- 二元一次方程组:解法(代入法、加减法)、应用(涉及两个未知量的问题)。
- 一元二次方程
- 解法:直接开平方法、配方法、公式法、因式分解法。
- 根的判别式:$\Delta = b^2 - 4ac$,判断根的情况。
- 根与系数的关系:韦达定理($x_1+x_2=-\frac{b}{a}$, $x_1x_2=\frac{c}{a}$)。
- 应用:数字问题、几何问题、增长率问题等。
- 分式方程:解法(转化为整式方程)、必须验根(增根问题)。
- 思想方法:方程思想(用等量关系解决问题),转化思想,分类讨论思想(如分式方程验根)。
-
不等式(组)
- 一元一次不等式:性质、解法、在数轴上表示解集。
- 一元一次不等式组:解法、求公共解集、在数轴上表示解集。
- 应用:求范围、方案选择问题。
- 思想方法:数形结合思想(数轴表示解集),转化思想。
函数
函数是描述运动变化和数量关系的数学模型,是初中数学的难点和重点。
-
函数的基本概念
- 定义:变量、常量、自变量、因变量、函数。
- 表示方法:解析式法、列表法、图像法。
- 图像与性质:画函数图像的步骤(列表、描点、连线),函数值的意义。
-
一次函数
- 正比例函数:$y=kx$ (k≠0) 的图像(过原点的直线)和性质(k决定增减性)。
- 一次函数:$y=kx+b$ (k≠0) 的图像(直线)和性质(k决定增减性,b与y轴交点)。
- 待定系数法:利用两点坐标求解析式。
- 应用:解决行程、利润、方案优化等问题。
- 思想方法:数形结合思想(图像与性质结合),模型思想。
-
反比例函数
- 定义:$y=\frac{k}{x}$ (k≠0)。
- 图像与性质:双曲线,k决定图像所在象限和增减性。
- 应用:面积问题($S=\frac{|k|}{2}$)等。
-
二次函数
- 定义:$y=ax^2+bx+c$ (a≠0)。
- 图像与性质:抛物线,开口方向(a)、对称轴($x=-\frac{b}{2a}$)、顶点坐标($(-\frac{b}{2a}, \frac{4ac-b^2}{4a})$)、增减性、最值。
- 解析式的求法:
- 一般式:$y=ax^2+bx+c$ (利用三点坐标)。
- 顶点式:$y=a(x-h)^2+k$ (利用顶点和另一点)。
- 交点式:$y=a(x-x_1)(x-x_2)$ (利用与x轴交点)。
- 应用:最值问题(利润最大、高度最高)、与几何图形结合的综合题。
- 思想方法:数形结合思想(核心),配方法,转化思想。
第二部分:图形与几何
几何学习旨在培养学生的空间想象能力、逻辑推理能力和几何直观。
图形的认识
-
基本图形
- 直线、射线、线段:概念、表示、性质、公理(两点之间线段最短)。
- 角:概念、分类、度量、相关的角(余角、补角、对顶角)。
- 相交线与平行线:三线八角(同位角、内错角、同旁内角),平行线的判定与性质,平移。
-
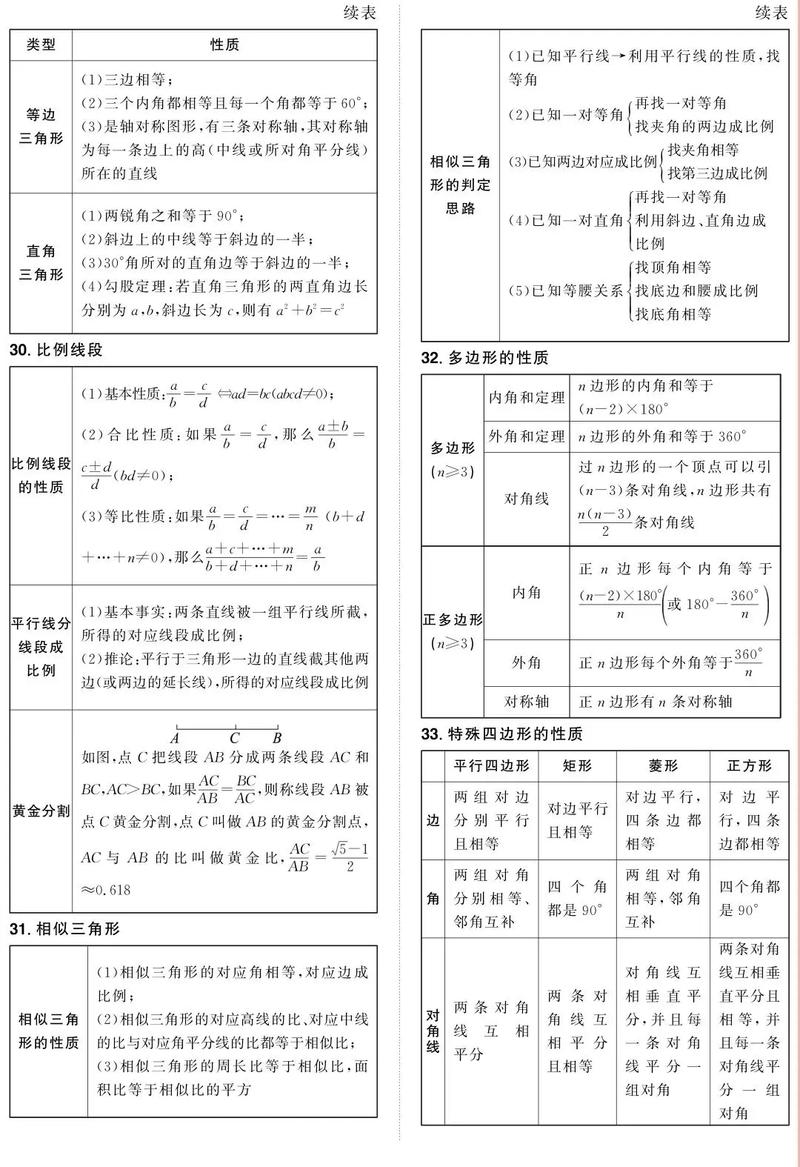
三角形
- 概念:内角和(180°)、三边关系(两边之和大于第三边)。
- 全等三角形:判定公理(SAS, ASA, AAS, SSS)和定理(HL for Rt. Δ),性质。
- 特殊三角形:等腰三角形(三线合一)、等边三角形(60°角)的性质与判定。
- 相似三角形:定义,判定定理(AA, SAS, SSS),性质(对应角相等,对应边成比例),相似比。
- 解直角三角形:锐角三角函数(正弦、余弦、正切),特殊角的三角函数值,解直角三角形及其应用(仰角、俯角、坡角等)。
-
四边形
- 平行四边形:性质与判定(边、角、对角线)。
- 矩形、菱形、正方形:它们之间的包含关系,各自的性质与判定。
- 梯形:等腰梯形的性质与判定。
-
圆
- 基本概念:圆心、半径、直径、弦、弧、圆心角、圆周角。
- 性质:垂径定理,圆心角、弧、弦之间的关系,圆周角定理及其推论。
- 点、直线、圆与圆的位置关系:数量关系的判断。
- 正多边形与圆:计算正多边形的边长、半径、边心距、面积。
- 弧长和扇形面积:计算公式。
- 思想方法:转化思想(圆内问题转化为三角形问题),数形结合,分类讨论。
图形与变换
-
轴对称
- 性质:对应点所连线段被对称轴垂直平分。
- 应用:等腰三角形、角的轴对称性。
-
平移
- 性质:对应点所连线段平行且相等。
- 应用:平行四边形的判定。
-
旋转
- 性质:对应点到旋转中心的距离相等,对应点与旋转中心的连线所成的角相等。
- 应用:中心对称图形(如平行四边形、圆)。
尺规作图
掌握基本作图:作一条线段等于已知线段、作一个角等于已知角、作角的平分线、作线段的垂直平分线、过一点作已知直线的垂线等。
第三部分:统计与概率
强调数据处理和随机观念的培养。
统计
- 数据收集与整理:总体、个体、样本、样本容量,抽样调查,频数、频率。
- 数据的描述
- 统计图:条形图、扇形图、折线图、直方图的特点和应用。
- 数据代表:平均数(加权平均数)、中位数、众数的意义和计算。
- 数据波动:极差、方差的意义和计算(方差越大,数据越不稳定)。
- 统计的简单应用:根据统计图表获取信息,进行简单的分析、判断和预测。
概率
- 基本概念:必然事件、不可能事件、随机事件。
- 古典概型:计算公式 $P(A)=\frac{m}{n}$ (m是事件A包含的结果数,n是所有等可能的结果数)。
- 几何概型:利用面积、长度等计算概率。
- 概率的简单应用:用概率解释生活现象,进行简单的决策。
第四部分:综合与实践
这是一个相对开放的领域,旨在将数学知识应用于解决实际问题。
- 特点:问题情境真实,具有综合性、探究性、开放性。
- 常见类型:方案设计问题、测量问题、最优化问题、规律探究问题等。
- 核心能力:阅读理解能力、信息提取能力、建模能力、分析问题和解决问题的能力。
第五部分:核心数学思想方法
这是数学的灵魂,是解决一切数学问题的“内功”。
- 数形结合思想:将“数”与“形”结合起来分析、解决问题,用数轴表示有理数,用函数图像研究函数性质,用几何图形解决代数问题。
- 转化与化归思想:将未知问题转化为已知问题,复杂问题转化为简单问题,解分式方程转化为整式方程,求不规则图形面积转化为规则图形面积。
- 分类讨论思想:当研究对象包含多种可能性时,需要根据其属性分成若干类逐一研究,讨论含绝对值的方程,讨论含参数的函数图像。
- 函数与方程思想:用运动、联系、变化的观点分析问题,通过建立函数关系或方程模型解决问题。
- 整体思想:将问题的某一部分看成一个整体来处理,在因式分解、代数式求值中经常使用。
- 模型思想:从现实生活或具体情境中抽象出数学问题,用数学语言表达和解决。
教学建议
- 注重概念的形成过程:不仅要让学生记住定义,更要理解其内涵和外延。
- 强调知识间的联系:帮助学生构建知识网络,如方程与函数的联系,相似三角形与解直角三角形的联系。
- 突出数学思想方法的渗透:在解题教学和概念教学中,有意识地引导学生运用数学思想方法。
- 加强应用意识和实践能力:多设计贴近生活的案例,鼓励学生动手操作、合作探究。
- 关注学生差异:设计不同层次的练习,让每个学生都能在原有基础上获得发展。
这份知识体系希望能为你提供一个清晰的框架,在实际学习和教学中,还需要不断深化、细化,并结合具体的例题和练习来巩固和理解。