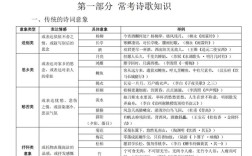
初中数学学习需要掌握科学的方法,才能有效提升解题能力和思维水平,以下是17种实用的初中数学学习方法,结合具体操作步骤和示例进行说明,帮助学生系统掌握数学学习技巧。

-
概念理解法
数学概念是解题的基础,需通过定义、公式、定理的深入理解掌握核心内涵,学习“一次函数”时,需明确其解析式y=kx+b(k≠0)中k、b的几何意义,结合图像理解斜率与截距的实际含义,可通过画图、举例(如路程与时间的关系)强化记忆。 -
公式推导法
死记硬背公式易遗忘,主动推导可加深理解,平方差公式(a+b)(a-b)=a²-b²可通过多项式乘法展开验证,或用几何图形(边长为a、b的正方形面积差)直观展示。 -
错题整理法
建立错题本,分类记录错误原因(如概念混淆、计算失误),并标注正确解法,每周复习错题,重点攻克高频错误类型,如分式方程忘记验根、二次函数顶点坐标公式记错等。 -
思维导图法
用思维导图梳理章节知识体系,学习“三角形”时,可从“分类(按角/边)—性质(内角和、三边关系)—判定(全等/相似)”三个维度展开,形成知识网络。 (图片来源网络,侵删)
(图片来源网络,侵删) -
一题多解法
尝试用不同方法解决同一问题,培养发散思维,证明“线段垂直平分线上的点到两端点距离相等”,可用全等三角形、坐标法(建立直角坐标系)或几何变换(对称)等多种途径。 -
模型构建法
将复杂问题转化为数学模型,行程问题中的“相遇追及”可抽象为s=vt的方程模型,工程问题用“单位时间工作量”表示效率。 -
数形结合法
利用图形辅助理解抽象问题,解一元二次方程时,通过函数图像与x轴的交点判断根的个数;学习绝对值概念时,借助数轴理解其几何意义。 -
归纳总结法
对同类题型总结规律,在“圆”的计算中,归纳弧长、扇形面积、圆锥侧面积的公式共性(均与圆周率、半径、圆心角相关)。 (图片来源网络,侵删)
(图片来源网络,侵删) -
分类讨论法
根据条件可能出现的所有情况分类求解,讨论含绝对值的方程|x-2|=a时,需分a>0、a=0、a<0三种情况分析。 -
逆向思维法
从结论倒推条件,几何证明中若需证“两直线平行”,可联想判定方法(同位角相等、内错角相等等),逆向寻找已知条件。 -
类比联想法
通过新旧知识对比学习,学习“分式”时,可与“分数”类比,从基本性质、运算法则到约分通分,降低理解难度。 -
实际应用法
结合生活场景理解数学,用概率知识解释彩票中奖率,用统计图表分析班级成绩分布,增强学习兴趣。 -
限时训练法
模拟考试环境进行限时练习,提升解题速度和应试能力,用45分钟完成一套“二次函数”综合题,重点训练时间分配。 -
小组讨论法
与同学合作探究难题,通过讲解和辩论深化理解,共同解决“动态几何问题”时,分工画图、计算、验证,提高效率。 -
口诀记忆法
将复杂知识点编成口诀,记特殊角三角函数值可用“正弦三十度二分之一,余弦三十度根号三之二”等顺口溜。 -
步骤拆解法
将复杂问题拆分为简单步骤,解分式方程时,按“去分母—去括号—移项—合并同类项—检验”的步骤逐步求解。 -
错题重练法
针对错题定期重新练习,确保真正掌握,每周从错题本中选取5道题重新解答,检验是否再次出错。
以下是部分方法的具体操作示例表格:
| 方法名称 | 适用场景 | 操作步骤 | 示例 |
|---|---|---|---|
| 概念理解法 | 新知识学习 | 阅读定义;2. 画图举例;3. 对比辨析 | 学习“相似三角形”时,用放大缩小的三角形实例理解对应角相等、对应边成比例 |
| 错题整理法 | 复习阶段 | 抄录错题;2. 标注错误原因;3. 写正确解法;4. 定期复习 | 计算(a+b)²时误记为a²+b²,需补充完全平方公式(a+b)²=a²+2ab+b² |
| 数形结合法 | 函数与几何 | 画图;2. 标注关键点;3. 结合图形分析 | 解不等式组x>1且x<3时,在数轴上标出解集 |
相关问答FAQs
Q1:如何避免数学考试中因粗心丢分?
A1:可通过以下方法减少粗心错误:①书写工整,步骤清晰,避免跳步;②做完后快速检查关键步骤(如符号、单位、计算结果);③建立“易错点清单”,考前重点复习;④审题时圈画关键词(如“至少”“不大于”),避免理解偏差。
Q2:数学基础差的学生如何快速提高成绩?
A2:建议分三步走:①补基础:从课本例题和基础题入手,掌握核心概念和公式(如一元一次方程、三角形性质);②重方法:学习上述17种方法中的概念理解、错题整理、模型构建等基础方法;③勤练习:每天做5-10道题,由易到难,逐步提升信心,同时可寻求老师或同学帮助,针对性解决薄弱环节。